I remember how I was happy when I find the integration of the Gaussian function in my high school years. It was an instantaneous spark which make me realize that increasing the integration dimension may bring a solution. Moreover, one can find a series expansion for Pi number after evaluating the integral.

Gaussian Integral

What is the Gaussian integral: Finding the area under the Gaussian function.

\[I = \int_{-\infty}^{+\infty}\, e^{-\alpha x^2}\,dx\]
Figure 1: Gaussian(x) = exp(-x^2)

There is no known function whose derivative is equal to Gaussian . Therefore, we need something different to get an answer for this integration.
Let’s define another integral in 2-D:

\[\hat I = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} e^{-\alpha (x^2+y^2)}\,dx\,dy\]

Because the integration domain is all real space in 2D and exponential function is separable,  x and y may be integrated independently.

\[\hat I = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} e^{-\alpha (x^2+y^2)}\,dx\,dy = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} e^{-\alpha x^2} e^{-\alpha y^2} \,dx\,dy = \bigg(\int_{-\infty}^{+\infty}e^{-\alpha x^2} \,dx\bigg) \bigg(\int_{-\infty}^{+\infty}e^{-\alpha y^2} \,dy\bigg)\]

This equation says that \(\hat I = I^2\). If we can find a method to calculate \(\hat I\), we can solve our problem. \(\hat I\) simply calculates volume under the \({e^{-\alpha (x^2+y^2)}}\) function. Alternatively, we can calculate same volume with cylindrical coordinates by summing infinitesimal cylindrical volume elements \(f(r{,}\theta)rd\theta dr\) where  \({r^2=x^2+y^2} , {\theta=\arctan(\frac{y}{x})}\). What this actually means is that you can calculate the volume under the lovely Gaussian blanket by summing either infinitesimal rectangular boxes or infinitesimal cylindrical boxes.

Figure 2: Gaussian(x,y) = exp(-x^2-y^2)
\[\hat I =\int_{0}^{2\pi} \int_{0}^{+\infty} e^{-\alpha r^2}\,dr\,rd\theta\]

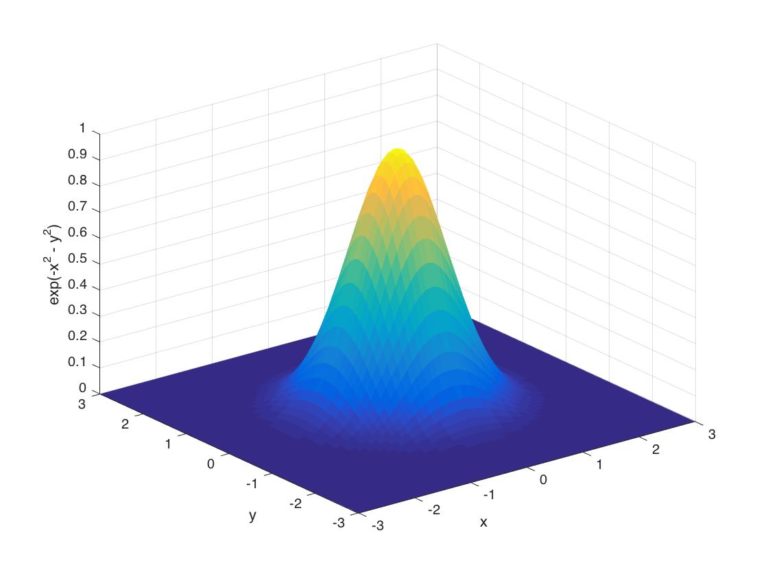
Now, we can integrate this:

\[\hat I = {\int_{0}^{2\pi}d\theta} {\int_{0}^{+\infty} e^{-\alpha r^2}\, \frac{d(r^2)}{2}}\]

All integrals can be done with known functions:

\[\hat I = (\theta |_{0}^{2\pi})(\frac{e^{-\alpha r^2}}{2\alpha}\bigg|_{0}^{+\infty} ) = \frac{\pi}{\alpha}\]

Then, the beautiful answer for our Gaussian integral which connects \(e\) to \(\pi\)

\[{\int_{-\infty}^{+\infty} e^{-\alpha x^2}\,dx} = \sqrt[]{\frac{\pi}{\alpha} }\]

Pi Approximator

If \(\alpha = 1\), we have: \(\sqrt[]{\pi} = {\int_{-\infty}^{+\infty} e^{-x^2}\,dx}\)

We can expand exponential to its Taylor series:

\[e^{u} = 1 + u + \frac{u^2}{2} + ... = \sum\limits_{n=0}^{\infty} {\frac{u^n}{n!}}\Rightarrow e^{-x^2}=1 - x^2 + \frac{x^4}{4} + ... = \sum\limits_{n=0}^{\infty} {({-1})^n \frac{x^{2n}}{n!}}\]

Thus, we can evaluate the integral with this expansion:

\[{\int_{-\infty}^{+\infty} e^{-x^2}\,dx}={\int_{-\infty}^{+\infty}\sum\limits_{n=0}^{\infty} {({-1})^n \frac{x^{2n}}{n!}}\,dx}={\sum\limits_{n=0}^{\infty} {({-1})^n \frac{x^{2n+1}}{(2n+1)n!}}}\bigg|_{-\infty}^{+\infty}\]

Finally we have exact expression for \(pi\):

\[\pi = \bigg(\sum\limits_{n=0}^{\infty} {({-1})^n \frac{x^{2n+1}}{(2n+1)n!}}\bigg|_{-\infty}^{+\infty}\bigg)^2\]

To numerically calculate this, we should approximate this expression. This is equal to assigning all infinities to a finite number:

\[\pi\approx\bigg(\sum\limits_{n=0}^{k} {({-1})^n \frac{x^{2n+1}}{(2n+1)n!}}\bigg|_{-a}^{+a}\bigg)^2\]

One thing to notice is if we increase \(a\), we should increase \(k\) much faster in order to get convergence. Increasing \(a\) and \(k\) will cause more floating point error in computation. Therefore, we need to find ideal \(a\), then a large enough \(k\). In Figure 1, we can see that exponential is very small after \(\|x\| \geq 3\). With these observations, I tried some \(a\) and \(k\). Eventually, I got a pi approximation with 8 decimal point accuracy. You can try it with below code:

function my_pi(a=4.5,k=70.0)
    total = 0.0
    for n=0:k
        total = total + (-1)^n * a^(2n+1)/((2n+1)*factorial(n))
    end
    return (2*total)^2 #total includes only +a part of the integration. Thus, we doubled it here. 
end

julia > my_pi(a=4.5,k=70.0)
3.141592659154459

julia > pi
π = 3.1415926535897...

Further Reading